◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--1-plane-geometry / Proposition: 1.19: Angles and Sides in a Triangle II

Proposition: 1.19: Angles and Sides in a Triangle II

(Proposition 19 from Book 1 of Euclid's “Elements” - this a the conversion to the proposition 1.18)

In any triangle, the greater angle is subtended by the greater side.

• Let $ABC$ be a triangle having the angle $ABC$ greater than $BCA$.
• I say that side $AC$ is also greater than side $AB$.

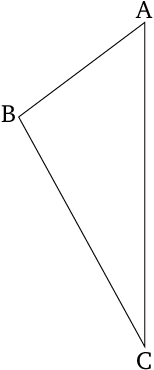
Modern Formulation

In a given triangle \(\triangle{ABC}\) with the angle \(\angle{ABC}\) greater than the angle \(\angle{BCA}\), the side \(\overline{AC}\) opposite to the greater angle is longer than \(\overline{AB}\), opposite to the smaller angle.

Table of Contents

Proofs: 1

Mentioned in:

Proofs: 1 2 3 4 5

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Calahan

@Casey

@Fitzpatrick

References

Adapted from CC BY-SA 3.0 Sources:

1. Callahan, Daniel: "Euclid’s 'Elements' Redux" 2014

Adapted from (Public Domain)

1. Casey, John: "The First Six Books of the Elements of Euclid"

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"