◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--1-plane-geometry / Proposition: 1.31: Constructing a Parallel Line from a Line and a Point

Proposition: 1.31: Constructing a Parallel Line from a Line and a Point

Euclid's Formulation

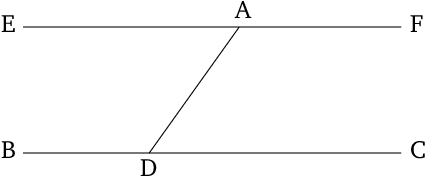
To draw a straight line parallel to a given straight line, through a given point.

• Let $A$ be the given point, and $BC$ the given straight line.
• So it is required to draw a straight line parallel to the straight line $BC$, through the point $A$.

Modern Formulation

Given a straight line \(BC\) and a point \(A\), which does not lie on the line, it is possible to construct the straight line \(EF\), which is parallel to \(BC\) and goes through the point $A.$

Table of Contents

Proofs: 1

Mentioned in:

Proofs: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
Sections: 27

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Calahan

@Casey

@Fitzpatrick

References

Adapted from CC BY-SA 3.0 Sources:

1. Callahan, Daniel: "Euclid’s 'Elements' Redux" 2014

Adapted from (Public Domain)

1. Casey, John: "The First Six Books of the Elements of Euclid"

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"