◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--1-plane-geometry / Proposition: 1.22: Construction of Triangles From Arbitrary Segments

Proposition: 1.22: Construction of Triangles From Arbitrary Segments

(Proposition 22 from Book 1 of Euclid's “Elements”)

To construct a triangle from three straight lines which are equal to three given [straight lines]. It is necessary for (the sum of) two (of the straight lines) taken together in any (possible way) to be greater than the remaining (one), [on account of the (fact that) in any triangle (the sum of) two sides taken together in any (possible way) is greater than the remaining (one) [Prop. 1.20] ].

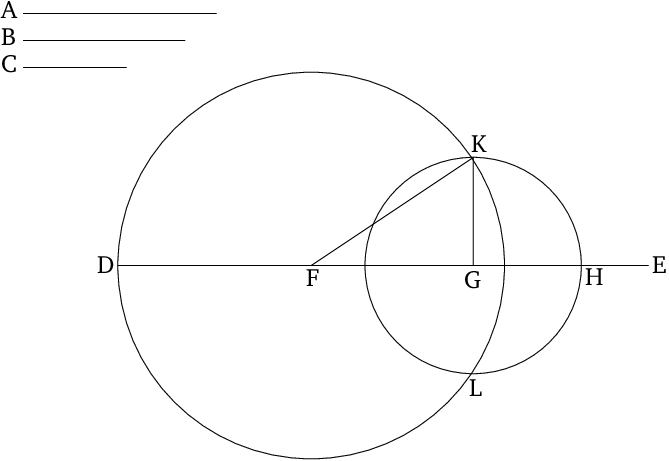
• Let $A$, $B$, and $C$ be the three given straight lines, of which let (the sum of) two taken together in any (possible way) be greater than the remaining (one).
• (Thus), (the sum of) $A$ and $B$ (is greater) than $C$, (the sum of) $A$ and $C$ than $B$, and also (the sum of) $B$ and $C$ than $A$.
• So it is required to construct a triangle from (straight lines) equal to $A$, $B$, and $C$.

Modern Formulation

If for three arbitrary segments $A=\overline{DF}$, $B=\overline{FG}$, and $C=\overline{GH}$, the sum of every two pairs of segments is greater than the length of the remaining segment, then it is possible¹ to construct a triangle, whose three sides are respectively equal to the three segments.

Table of Contents

Proofs: 1

Mentioned in:

Proofs: 1
Sections: 2

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Calahan

@Casey

@Fitzpatrick

References

Adapted from CC BY-SA 3.0 Sources:

1. Callahan, Daniel: "Euclid’s 'Elements' Redux" 2014

Adapted from (Public Domain)

1. Casey, John: "The First Six Books of the Elements of Euclid"

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"

Footnotes