Let \(\angle{ABC}\) and \(\angle{PQR}\) be two angles. The sum of these angles \[\angle{ABR}:=\angle{ABC} + \angle{PQR}\] is the angle \(\angle{ABR}\), if the leg \(\overline{QP}\) is applied to the leg \(\overline{BC}\), such that the vertex \(Q\) falls on the vertex \(B\) and the leg \(\overline{QR}\) falls on the opposite side of \(\overline{BC}\) from \(\overline{BA}\).
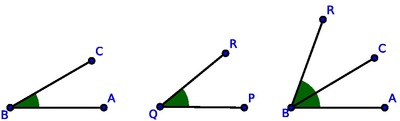
Since the sum of two angles is again an angle, we can sum more then two angles by adding each next angle to the previously built sum.
Corollaries: 1