◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--1-plane-geometry / Proposition: 1.26: "Angle-Side-Angle" and "Angle-Angle-Side" Theorems for the Congruence of Triangles
Proposition: 1.26: "Angle-Side-Angle" and "Angle-Angle-Side" Theorems for the Congruence of Triangles
(Proposition 26 from Book 1 of Euclid's “Elements”)
If two triangles have two angles equal to two angles, respectively, and one side equal to one side - in fact, either that by the equal angles, or that subtending one of the equal angles - then (the triangles) will also have the remaining sides equal to the [corresponding] remaining sides, and the remaining angle (equal) to the remaining angle.
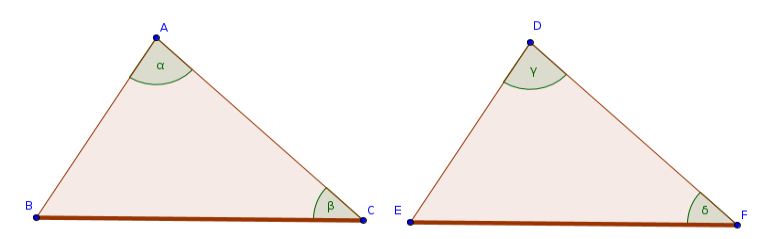
- Let $ABC$ and $DEF$ be two triangles having the two angles $ABC$ and $BCA$ equal to the two (angles) $DEF$ and $EFD$, respectively. (That is) $ABC$ (equal) to $DEF$, and $BCA$ to $EFD$.
- And let them also have one side equal to one side.
- First of all, the (side) by the equal angles. (That is) $BC$ (equal) to $EF$.
- I say that they will have the remaining sides equal to the corresponding remaining sides. (That is) $AB$ (equal) to $DE$, and $AC$ to $DF$.
- And (they will have) the remaining angle (equal) to the remaining angle. (That is) $BAC$ (equal) to $EDF$.

Modern Formulation
If two triangles (\(\triangle{ABC}\), \(\triangle{DEF}\)) have two angles of one (\(\alpha:=\angle{BAC}\), \(\beta:=\angle{ACB}\)) respectively equal to two angles of the other (\(\gamma:=\angle{EDF}\), \(\delta:=\angle{DFE}\)), and a side of one equal to a similarly placed side of the other (placed with regard to the angles), then both triangles are congruent \[\triangle{ABC}\cong\triangle{DEF}.\]
This proposition breaks down into two cases according to whether the equal sides are adjacent or opposite to the equal angles:
Case 1: "ANGLE-SIDE-ANGLE" theorem for the congruence of triangles
If the side in question is the side between the two angles, then the triangles are congruent.

Case 2: "ANGLE-ANGLE-SIDE" theorem for the congruence of triangles
If the side in question is not the side between the two angles, then the triangles are congruent.
respectively
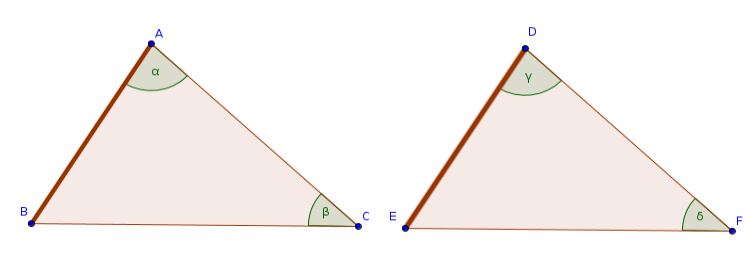
Table of Contents
Proofs: 1
Mentioned in:
Proofs: 1 2 3 4 5 6 7 8 9 10
Sections: 11
Thank you to the contributors under CC BY-SA 4.0! 

- Github:
-

- non-Github:
- @Calahan
- @Casey
- @Fitzpatrick
References
Adapted from CC BY-SA 3.0 Sources:
- Callahan, Daniel: "Euclid’s 'Elements' Redux" 2014
Adapted from (Public Domain)
- Casey, John: "The First Six Books of the Elements of Euclid"
Adapted from (subject to copyright, with kind permission)
- Fitzpatrick, Richard: Euclid's "Elements of Geometry"



