◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--1-plane-geometry / Proposition: 1.39: Triangles of Equal Area III

Proposition: 1.39: Triangles of Equal Area III

(Proposition 39 from Book 1 of Euclid's “Elements”)

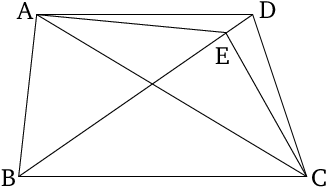
Equal triangles which are on the same base, and on the same side, are also between the same parallels.

• Let $ABC$ and $DBC$ be equal triangles which are on the same base $BC$, and on the same side (of it).
• I say that they are also between the same parallels.

Modern Formulation

Triangles (\(\triangle{BAC}\), \(\triangle{BDC}\)), which are equal in area and stand on the same base (\(\overline{BC}\)) and on the same side of the base also stand between the same parallels (\(\overline{AD}\), \(\overline{BC}\)).

Table of Contents

Proofs: 1

Mentioned in:

Proofs: 1

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Calahan

@Casey

@Fitzpatrick

References

Adapted from CC BY-SA 3.0 Sources:

1. Callahan, Daniel: "Euclid’s 'Elements' Redux" 2014

Adapted from (Public Domain)

1. Casey, John: "The First Six Books of the Elements of Euclid"

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"