◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--1-plane-geometry / Proposition: 1.07: Uniqueness of Triangles

Proposition: 1.07: Uniqueness of Triangles

(Proposition 7 from Book 1 of Euclid's “Elements”)

On the same straight line, two other straight lines equal, respectively, to two (given) straight lines (which meet) cannot be constructed (meeting) at a different point on the same side (of the straight line), but having the same ends as the given straight lines.

Modern Formulation

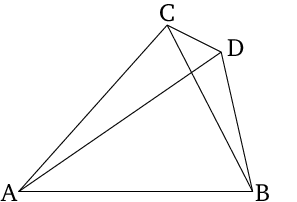
Suppose two distinct triangles \(\triangle{ABC}\) and \(\triangle{ABD}\) share a common base \(\overline{AB}\) and lie on the same side of it. Also suppose that at one endpoint of the base, e.g. \(A\), the two sides connecting to \(A\) are equal in length: \(\overline{AC}=\overline{AD}\). Then the lengths of the sides connected to the other endpoint of the base (point $B$), are unequal in length: \(\overline{BC}\neq\overline{BD}\).

Table of Contents

Proofs: 1

Mentioned in:

Motivations: 1
Proofs: 2

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Calahan

@Casey

@Fitzpatrick

References

Adapted from CC BY-SA 3.0 Sources:

1. Callahan, Daniel: "Euclid’s 'Elements' Redux" 2014

Adapted from (Public Domain)

1. Casey, John: "The First Six Books of the Elements of Euclid"

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"