If some point is taken outside a circle, and some straight lines are drawn from the point to the (circumference of the) circle, one of which (passes) through the center, the remainder (being) random, then for the straight lines radiating towards the concave (part of the) circumference, the greatest is that (passing) through the center. For the others, a (straight line) nearer1 to the (straight line) through the center is always greater than one further away. For the straight lines radiating towards the convex (part of the) circumference, the least is that between the point and the diameter. For the others, a (straight line) nearer to the least (straight line) is always less than one further away. And only two equal (straight lines) will radiate from the point towards the (circumference of the) circle, (one) on each (side) of the least (straight line).
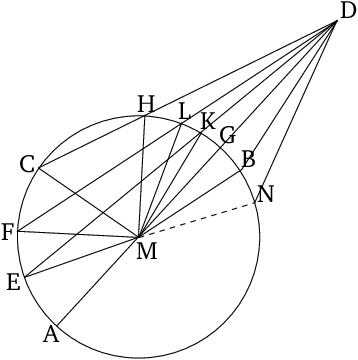
In the family of (infinitely many) segments connecting a point outside a circle ($D$) with all the points of its circumference there is exactly one, which is the longest (let it be $\overline{DA}$ with the length $\beta$), and there is exactly one, which is the shortest (let it be $\overline{DG}$ with the length $\alpha$). Both, the longest $\overline{DA}$ and the shortest $\overline{DG},$ lie on the same straight line $DA$, on which also the center of the circle ($M$) is located. Moreover, all other segments of this family have lengths $\gamma$ with a value between $\alpha\le\gamma\le\beta$ and there are exatly two of them having the same length $\gamma$, namely those lying symmetrically with respect to the straight line $DA.$
Proofs: 1
Presumably, in an angular sense (translator's note). ↩