Proposition: 5.17: Magnitudes Proportional Compounded are Proportional Separated

(Proposition 17 from Book 5 of Euclid's “Elements”)

If composed magnitudes are proportional then they will also be proportional (when) separated.

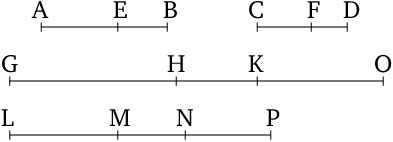
Let $AB$, $BE$, $CD$, and $DF$ be composed magnitudes (which are) proportional, (so that) as $AB$ (is) to $BE$, so $CD$ (is) to $DF$.
I say that they will also be proportional (when) separated, (so that) as $AE$ (is) to $EB$, so $CF$ (is) to $DF$.

fig17e

Modern Formulation

In modern notation, this proposition reads that if \[\frac{\alpha+\beta}\beta=\frac{\gamma+\delta}\delta,\] then \[\frac\alpha\beta=\frac\gamma\delta,\]

for all positive real numbers $\alpha,\beta,\gamma,\delta$.

Proofs: 1

Proofs: 1 2 3 4
Sections: 5

Thank you to the contributors under CC BY-SA 4.0!