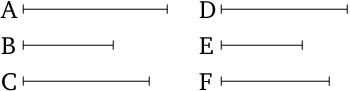Proposition: 5.20: Relative Sizes of Successive Ratios

(Proposition 20 from Book 5 of Euclid's “Elements”)

If there are three magnitudes, and others of equal number to them, (being) also in the same ratio taken two by two, and (if), via equality, the first is greater than the third then the fourth will also be greater than the sixth. And if (the first is) equal (to the third then the fourth will also be) equal (to the sixth). And if (the first is) less (than the third then the fourth will also be) less (than the sixth).

Let $A$, $B$, and $C$ be three magnitudes, and $D$, $E$, $F$ other (magnitudes) of equal number to them, (being) in the same ratio taken two by two, (so that) as $A$ (is) to $B$, so $D$ (is) to $E$, and as $B$ (is) to $C$, so $E$ (is) to $F$.
And let $A$ be greater than $C$, via equality.
I say that $D$ will also be greater than $F$.

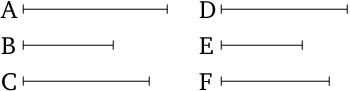
fig20e

Modern Formulation

In modern notation, this proposition reads that if \[\frac\alpha\beta=\frac\delta\epsilon\text{ and }\frac\beta\gamma=\frac\epsilon\zeta,\] then \[\alpha\gtreqqless\gamma~\text{ as }~\delta\gtreqqless\zeta,\]

for all positive real numbers $\alpha,\beta,\gamma,\delta,\epsilon,\zeta$.

Proofs: 1

Proofs: 1
Sections: 2

Thank you to the contributors under CC BY-SA 4.0!