Proposition: 6.27: Similar Parallelogram on Half a Straight Line

(Proposition 27 from Book 6 of Euclid's “Elements”)

Of all the parallelograms applied to the same straight line, and falling short by parallelogrammic figures similar, and similarly laid out, to the (parallelogram) described on half (the straight line), the greatest is the [parallelogram] applied to half (the straight line) which (is) similar to (that parallelogram) by which it falls short.

Let $AB$ be a straight line, and let it have been cut in half at (point) $C$ [Prop. 1.10].
And let the parallelogram $AD$ have been applied to the straight line $AB$, falling short by the parallelogrammic figure $DB$ (which is) applied to half of $AB$ - that is to say, $CB$.
I say that of all the parallelograms applied to $AB$, and falling short by [parallelogrammic] figures similar, and similarly laid out, to $DB$, the greatest is $AD$.

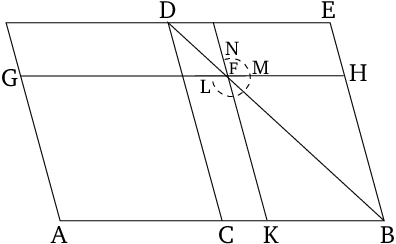
fig27e

Modern Formulation

Let a parallelogram ($\boxdot{AE}$) be bisected by the segment $\overline{DC}.$ For all points $F$ lying on the segment $\overline{DB}$, among the parallelogramic figures ($\boxdot{AF}$ like drawn above), the parallelogram $\boxdot{AD}$ has the greatest area.

Proofs: 1

Thank you to the contributors under CC BY-SA 4.0!