Proposition: 6.32: Triangles with Two Sides Parallel and Equal

(Proposition 32 from Book 6 of Euclid's “Elements”)

If two triangles, having two sides proportional to two sides, are placed together at a single angle such that the corresponding sides are also parallel, then the remaining sides of the triangles will be straight-on (with respect to one another).

Let $ABC$ and $DCE$ be two triangles having the two sides $BA$ and $AC$ proportional to the two sides $DC$ and $DE$ - so that as $AB$ (is) to $AC$, so $DC$ (is) to $DE$ - and (having side) $AB$ parallel to $DC$, and $AC$ to $DE$.
I say that (side) $BC$ is straight-on to $CE$.

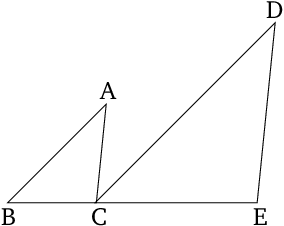
fig32e

Modern Formulation

If in two triangles ($\triangle{ABC},$ $\triangle{DCE}$) two corresponding sides are proportional $$\frac{|\overline{AB}|}{|\overline{AC}|}=\frac{|\overline{DC}|}{|\overline{DE}|}$$ and the triangles have a common edge ($C$), then the remaining sides ($\overline{BC},$ $\overline{CE}$ are collinear).

Proofs: 1

Thank you to the contributors under CC BY-SA 4.0!