◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--9-number-theory-applications / Proposition: Prop. 9.19: Condition for Existence of Fourth Number Proportional to Three Numbers

Proposition: Prop. 9.19: Condition for Existence of Fourth Number Proportional to Three Numbers

Euclid's Formulation

For three given numbers, to investigate when it is possible to find a fourth (number) proportional to them.

• Let $A$, $B$, $C$ be the three given numbers.
• And let it be required to investigate when it is possible to find a fourth (number) proportional to them.

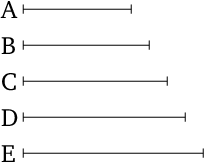
Modern Formulation

(not yet contributed)

Table of Contents

Proofs: 1

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Fitzpatrick

References

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"

Adapted from CC BY-SA 3.0 Sources:

1. Prime.mover and others: "Pr∞fWiki", https://proofwiki.org/wiki/Main_Page, 2016