Proof: By Euclid

For let the parallelepipedal solid $AB$ have been cut by the plane $CDEF$ (passing) through the diagonals of the opposite planes $CF$ and $DE$.¹
I say that the solid $AB$ will be cut in half by the plane $CDEF$.

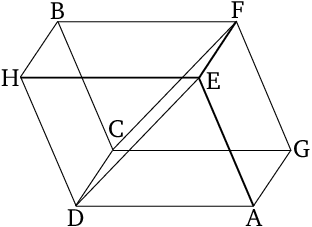
fig28e

For since triangle $CGF$ is equal to triangle $CFB$, and $ADE$ (is equal) to $DEH$ [Prop. 1.34], and parallelogram $CA$ is also equal to $EB$ - for (they are) opposite [Prop. 11.24] - and $GE$ (equal) to $CH$, thus the prism contained by the two triangles $CGF$ and $ADE$, and the three parallelograms $GE$, $AC$, and $CE$, is also equal to the prism contained by the two triangles $CFB$ and $DEH$, and the three parallelograms $CH$, $BE$, and $CE$.
For they are contained by planes (which are) equal in number and in magnitude " [Def. 11.10] ":https://www.bookofproofs.org/branches/equal-solid-figures/.²
Thus, the whole of solid $AB$ is cut in half by the plane $CDEF$.
(Which is) the very thing it was required to show.

∎

Thank you to the contributors under CC BY-SA 4.0!

Here, it is assumed that the two diagonals lie in the same plane. The proof is easily supplied (translator's note). ↩
However, strictly speaking, the prisms are not similarly arranged, being mirror images of one another (translator's note). ↩