◀ ▲ ▶Branches / Graph-theory / Example: A digraph with a loop, and parallel and inverse edges

Example: A digraph with a loop, and parallel and inverse edges

(related to Definition: Digraph, Initial and Terminal Vertices, Loops, Parallel and Inverse Edges, Simple Digraph)

The following digraphs demonstrate the concepts of the digraph definition:

Digraph \(D=(V,E,\alpha,\omega)\):

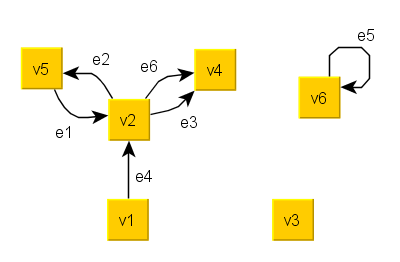
Vertices: \[V=\{v_1,v_2,v_3,v_4,v_5,v_6\}\]Edges:\[E=\{e_1,e_2,e_3,e_4,e_5\}\] Initial vertices:\[\alpha(e_1)=v_5,\alpha(e_2)=\alpha(e_3)=\alpha(e_6)=v_2, \alpha(e_4)=v_1, \alpha(e_5)=v_6\] Terminal vertices: \[\omega(e_1)=v_2,\omega(e_2)=v_5, \omega(e_3)=\omega(e_6)=v_4, \omega(e_4)=v_2, \omega(e_5)=v_6\]``\(e_1\) and \(e_2\) are inverse edges, while \(e_3\) and \(e_6\) are parallel edges. \(e_5\) is a loop. Vertex \(v_3\) has no adjacent edges. \(D\) is not a simple digraph, since it has loops, and it also has parallel edges.

Digraph \(D'=(V,E,\alpha,\omega)\):

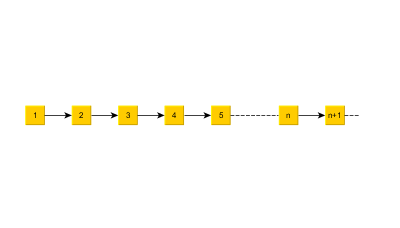
Vertices: \[V=\mathbb N\]Edges:\[E=\{(n,n+1),~~n\in\mathbb N\}\]Initial vertices:\[\alpha((n,n+1))=n~~~~\forall n\in\mathbb N\]Terminal vertices:\[\omega((n,n+1))=n+1~~~~\forall n\in\mathbb N\]There are no loops, no inverse and no parallel edges, thus \(D'\) is a simple digraph. However, it is infinite.