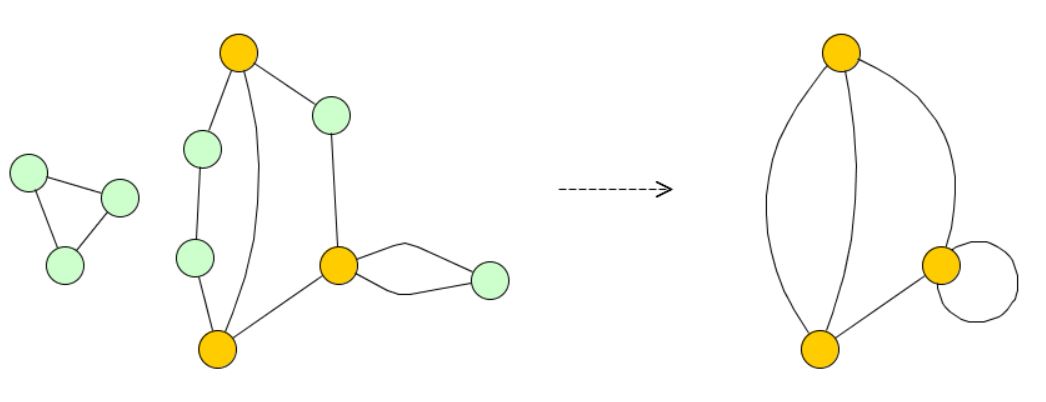
By suppressing vertices in an undirected graph \(G\) we mean the deleting of each vertex \(v\) of degree \(d_G(v)=2\) and adding an edge between its two neighbors. If the edges form a loop, we add no edge and obtain a graph without the vertex \(v\).
Since the degrees of all vertices other than those with degree \(d_G(v)=2\) remain unchanged, no matter in which order those vertices are suppressed, the obtained multigraph is well-defined and called the suppressed multigraph of \(G\), denoted by \(\tilde G\).
A multigraph \(G\) and its suppressed multigraph \(\tilde G\) - note that all blue vertices, which had degree \(2\) have been consecutively suppressed; independently of the order in which the vertices are suppressed, we always get the same suppressed multigraph: