We will prove later a result of Cantor (1845 - 1918) that the power set $\mathcal P(X)$ has always more elements than the original set $X$. This result is very important for the study of cardinals, we will be also talking about later. Loosely speaking, a cardinal is the number of elements of a set. Through this important result, Cantor was the first mathematician to notice that different infinite sets have different cardinals and thus starting with an infinite set $X$ and building the sets
$$X\rightarrow \mathcal P(X)\rightarrow \mathcal P(\mathcal P(X))\rightarrow\ldots$$
will create a never-ending hierarchy of infinite sets which become greater and greater. Moreover, this hierarchy is the starting point of the so-called continuum hypothesis - a fascinating hypothesis formulated by Georg Cantor (1845 - 1918) which he could not prove for the rest of his life. Thousands of mathematicians failed to prove it either until the continuum hypothesis was shown decades later to be undecidable in the set theory based only on the Zermelo-Fraenkel axioms. This means that it is not provable in contemporary mathematics, because the set theory is a basis of today's mathematics. But we will be talking about these fascinating topics in more detail later.
For the time being, we introduce another axiom established by Zermelo and Skolem independently of each other when they studied the above hierarchy of cardinals. They noticed that all axioms we have introduced so far are not sufficient to ensure the existence of a chain $X\rightarrow \mathcal P(X)\rightarrow \mathcal P(\mathcal P(X))\rightarrow\ldots$ This axiom is called the axiom of replacement.
For every predicate of the form1 $p(x,y,\overset{n}{x})$ the following axiom holds: For all $\overset{n}{x}$: If for every $x$ there is exactly one $y$ with $p(x,y,\overset{n}{x})$, then there is for every $u$ a set $w$ containing for every $x$ the element $y$ that fulfills $p(x,y,\overset{n}{x})$: $$\begin{array}{rl} \forall \overset{n}{x}\ni(&\\ &(\forall x\ni(\exists! y\ni p(x,y,\overset{n}{x})))\\ &\Rightarrow\\ &(\forall u\ni(\exists w\ni(\forall xy\ni(x\in u\wedge p(x,y,\overset{n}{x})\Rightarrow y\in w))))\\ ).& \end{array}$$ With the set-builder notation, this axiom justifies the existence (and with the axiom of extentionality the uniqueness) of a set $w$ being the image of a set $u$ under some function $\phi$ and some parameters $\overset{n}{x}$): $$\forall \overset{n}{x}\ni(\forall u\ni(\exists! w\ni (w=\{\phi(x,\overset{n}{x})\mid x\in u\}))).$$
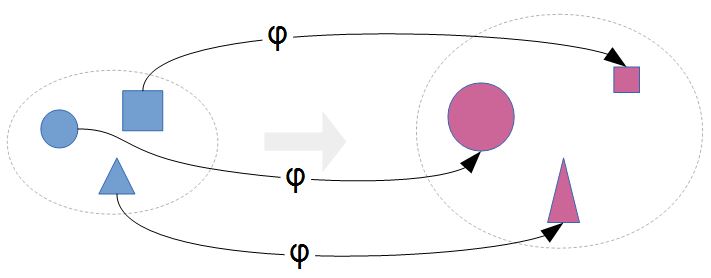
Axioms: 1
We abbreviate the tuple $x_1,\ldots,x_n$ by $\overset{n}{x}$. Since there are infinitely many such predicates, the axiom of replacement is, in fact, a schema for infinitely many axioms. ↩