(related to Chapter: Order Relations)
Please note that a maximum or minimum of $S$ do not have to exist. For instance, the chain of integers $(Z,\ge)$ neither has a maximum, nor a minimum. However, if a maximum or a minimum of $S$ exist, then they are unique, which follows immediately from their definition. For instance, if $g$ and $g'$ were two maxima, then $g\preceq g'$ and $g\succeq g'$ would follow by definition. Therefore, $g'=g,$ and thus $g$ is unique.
Every maximum (minimum) is also a maximal (minimal) element, but not vice versa! This is because a maximal (minimal) element only requires that there is no greater (smaller) element. But a maximum (minimum) requires that it is greater (smaller) or equal to all other elements.
The only difference between a maximum (minimum) $m$ and an upper (lower) bound $b$ of a set $S$ is that $m$ has to be an element of $S,$ while the bound $b$ can also be an element of $V\setminus S.$ For instance, $1$ is an upper bound of the set of all negative real numbers, but $1$ is not a negative real number. The same holds for the infimum and the supremum. To take the same example, $0$ is a supremum of all negative real numbers but it is still not a negative real number.
Below, a Hasse diagram of a simple poset $V:\{a,b,c,d,e,f,g\}$ is given, in which the elements of the subset $S=\{a,b,c,d,e\}$ are drawn as dark nodes:
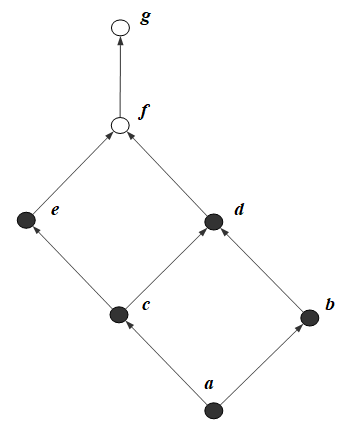
In this poset, the following observations can be made: * $g$ is a maximum of $V$ and, at the same time, its supremum, and its upper bound * $S$ has no maximum, but $d$ and $e$ are maximal in $S.$ * $g,f$ are upper bounds of $S$, therefore $\sup(S)=f.$ * $a$ is a minimum of $V$ and of $S.$ It is also a minimal element and an infimum of both sets.
Proofs: 1