(related to Part: Special Relativity)
In 1849, the French physicist Hippolyte Fizeau (1819 - 1896) showed that the speed of light is finite by measuring its speed. He let the light of a strong lantern pass trough two cogwheels, one of which was fixed and one of which could be rotated. The light passed the gaps between the teeth of the cogwheels exactly at the time, when they aligned each other. Otherwise, the light ray was interrupted by the teeth of the rotatable cogwheel. Whenever the light ray passed the cogwheels, it traversed the distance to a mirror placed about 8.6 kilometers away, then it returned and passed the cogwheels again to be observed by Fizeau. In sum, the light had to traverse the distance of about 17.2 kilometers.
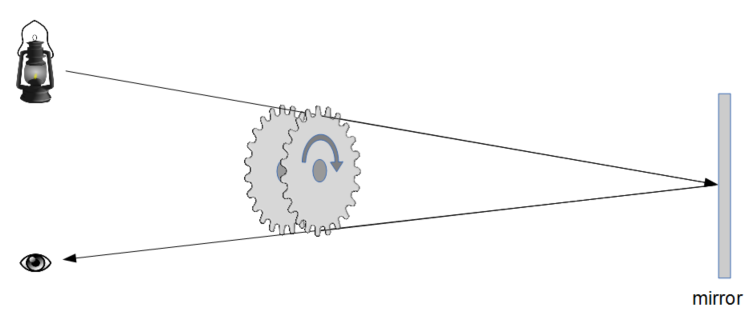
Picture by BookOfProofs: Own work
Fizeau observed that whenever the rotation of the rotatable cogwheel was fast enough, the mirror picture of the light in the lantern disappeared. This happened at about \(12.6\) to \(12.7\) rotations per second. Because both of Fizeau's cogwheels had exactly 720 teeth, he concluded that \(720\) teeth and \(720\) gaps between the teeth split one second into \[(720+720)\times 12.65=18,216\] (very short) time periods and that the light was still able to pass a gap between the teeth in those time periods, i.e. in \(1/18216\)-th of a second. Therefore, he concluded that the estimated speed of light is:
\[c\text{ (speed of light)}=\frac{\operatorname{distance}}{\operatorname{time}}=\frac{2\times 8.633\operatorname{km}}{\frac {1\operatorname{s}}{2\times 720\times 12.65}}=\frac{17.266\operatorname{km}\times 18,216}{1\operatorname{s}}\approx 314,500\frac{\operatorname{km}}{\operatorname{s}}.\]
Although this speed is very fast, Fizeau proved experimentally that the speed of light is finite.
Modern more precise measurements show that the speed of light is exactly
\[c=\cases{299,711 \frac{\operatorname{km}}{\operatorname{s}}&in the air\\ 299,792.458 \frac{\operatorname{km}}{\operatorname{s}}&in the vacuum.}\]