Let $(X,\mathcal O)$ be a topological space $X$ can be postulated to fulfill the following separation axioms:
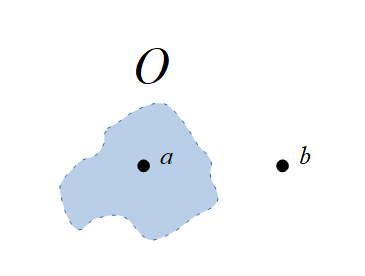
Among any two different points only one has an open set containing it, formally $$a,b\in X, a\neq b\Longrightarrow \exists O\in\mathcal O:\; (a\in O, b\not\in O)\vee (a\not\in O, b\in O).$$ In this case, $X$ is called a Kolmogorov space (Andrey Kolmogorov (1903 - 1987)).
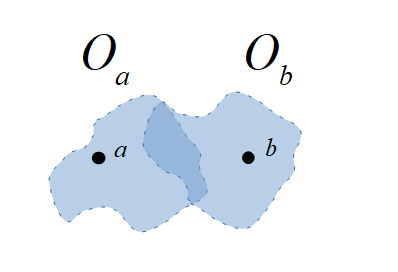
Among any two different points both have an open set containing only this point but not the other, formally $$a,b\in X, a\neq b\Longrightarrow \exists O_a,O_b\in\mathcal O:\; (a\in O_a, b\not\in O_a)\wedge (a\not\in O_b, b\in O_b).$$ In this case, $X$ is called a Fréchet space (René Maurice Fréchet (1878 - 1973)).
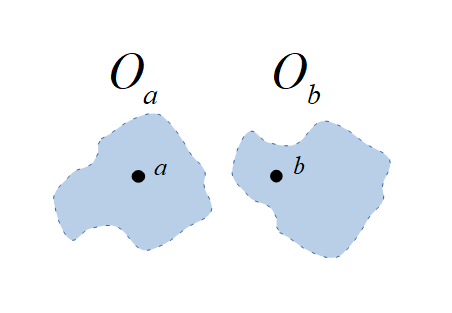
Two distinct points have to distinct open sets containing them, formally $$a,b\in X, a\neq b\Longrightarrow \exists O_a,O_b\in\mathcal O:\; (a\in O_a)\wedge (b\in O_b)\wedge (O_a\cap O_b=\emptyset).$$ In this case, $X$ is called a Hausdorff space (Felix Hausdorff (1868 - 1942)).
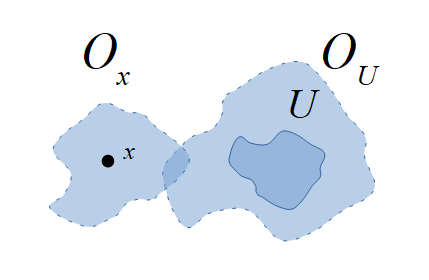
For every closed set and every point not contained in it there are open sets containing them respectively, formally $$x\not\in U\subset X\Longrightarrow \exists O_U,O_x\in\mathcal O:\; (U\subset O_U)\wedge (x\in O_x).$$ In this case, $X$ is called a Vietoris space (Leopold Vietoris (1891 - 2002)).
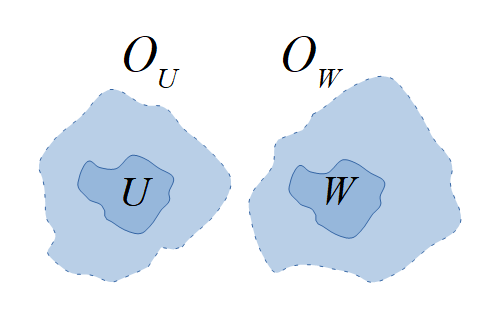
For any two disjoint closed sets there are disjoint open sets containing them, formally $$U,W\subset X\text{ closed }, U\cap W=\emptyset \Longrightarrow \exists O_U,O_W\in\mathcal O:\; (U\subset O_U)\wedge (W\subset O_W)\wedge (O_U\cap O_W=\emptyset).$$ In this case, $X$ is called a Tietze space (Franz Tietze (1880 - 1964)).
Definitions: 1 2
Proofs: 3 4 5
Propositions: 6 7 8 9