Definition: Topological Subspaces and Subspace Topologies

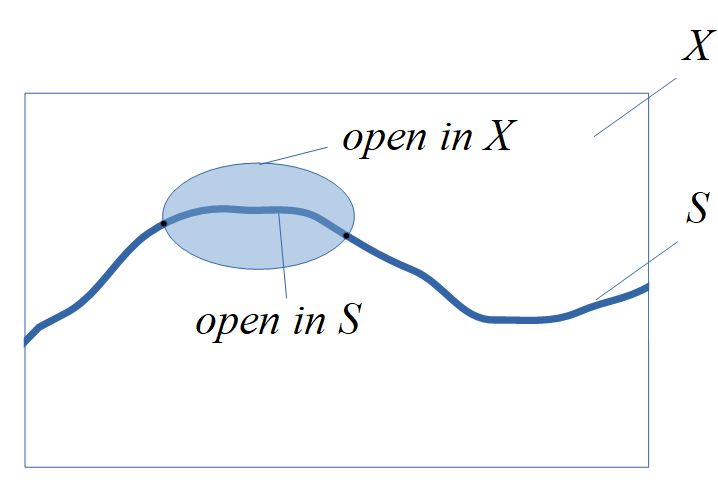
A subspace (or induced, or relative) topology $\mathcal O_S$ a topology induced by a given topological space $(X,\mathcal O)$ to all its subsets $S\subset X$, formally, the ordered pair defined by

$$(S,\mathcal O_S):=\begin{cases}S\subseteq X,\\\mathcal O_S=\{U\cap S\mid U\in\mathcal O\}\end{cases}$$

is the topological subspace of $(X,\mathcal O)$ induced by the topology $\mathcal O.$