(related to Corollary: Barycentric Coordinates, Barycenter)
Let \(\mathcal A=(A,V_A,v)\) be an affine space with \(V_A\) as the associated vector space over a field \(F\) . Take any \(Q\in \mathcal A\). By definition of an affine space there is a unique vector \(q\in V_A\) defined by \(q:=\overrightarrow{QP_0}\), which is equivalent to \(Q=P_0 + q\).
By hypothesis, \(P_0,P_1,P_2\ldots,P_n\) is an affine basis of \(\mathcal A\), which by definition means that the vectors \(x_1=\overrightarrow{P_0P_1},\,x_2=\overrightarrow{P_0P_2},\,\ldots,\,x_n=\overrightarrow{P_0P_n}\) form a basis of the corresponding vector space \(V_A\).
By definition of a basis of a vector space it means that there exist unique elements \(\lambda_1, \ldots, \lambda_n\in F \) such that \[q=\lambda_1x_1+ \cdots +\lambda_nx_n.\]
Then it follows
\[\begin{array}{rcl} Q&=&P_0+q\\ &=&P_0+\lambda_1x_1+\cdots+\lambda_nx_n\\ &=&P_0+\lambda_1\overrightarrow{P_1P_0}+\cdots+\lambda_n\overrightarrow{P_nP_0}\\ &=&P_0+\lambda_1(P_1-P_0)+\cdots+\lambda_n(P_n-P_0)\\ &=&P_0+\lambda_1P_1+\cdots+\lambda_nP_n -\lambda_1P_0-\cdots-\lambda_nP_0\\ &=&(1-(\lambda_1+\cdots+\lambda_n))P_0+\lambda_1P_1+\cdots+\lambda_nP_n\\ &=&\lambda_0P_0+\lambda_1P_1+\cdots+\lambda_nP_n \end{array}\] with \(\lambda_0:=1-(\lambda_1+\cdots+\lambda_n)\in F\).
Because all \(\lambda_0, \ldots, \lambda_n\in F \) form a unique \((n+1)\)-tuple, it follows
\[Q=\lambda _{0}P_{0}+\cdots +\lambda_{n}P_{n},\quad\quad\lambda_0+\cdots+\lambda_n=1.\]
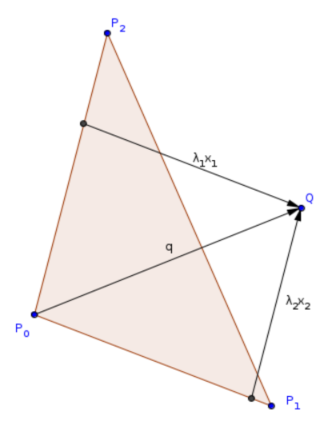
The following figure demonstrates the ideas of this proof for the special case of an affine plane, in which any point \(Q\) can be represented in barycentric coordinates using the affine basis of points of a triangle.
(c) bookofproofs own work