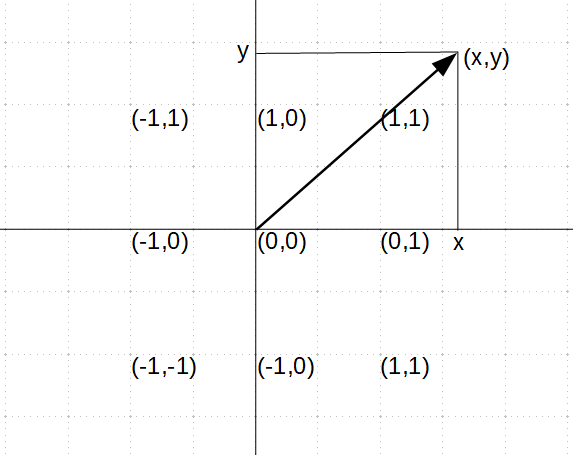(related to Definition: Vector Space)
The field of real numbers can be considered as a vector space over itself. We can add its vectors (adding real numbers) and we multiply them by a scalar (another real number).
From a geometrical point of view, the vector space $\mathbb R^1$ can be imagined as a number line. the following figure shows the number line vector space and a vector in it (here the number $3.5$):
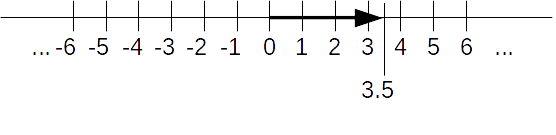
The number line has a designated vector, the zero vector $(0)$, and each point on the number line can be identified with the vector "pointing" to the real number $x$, which we can write as $(x)$.
René Descartes was the first to identify the points of a plane with pairs of two real numbers. As in the case of a number line, this requires the choice of a special vector, which is the zero vector $(0,0)$. Then, each point in the plane with the coordinates $x$ and $y$ can be identified with a vector pointing to the point, which has the same coordinates, i.e. the vector $(x,y).$