◀ ▲ ▶Branches / Analysis / Branch: Analysis

Branch: Analysis

Analysis is a broad area of mathematics studying the special properties of real-valued or complex-valued functions under the basic ideas of calculus like limits, continuity, differentiation, integration, or holomorphy. The key common feature of calculus is to combine infinitely many infinitely small (i.e. infinitesimal) quantities to get a finite answer. As an example, suppose we want to calculate the area of a circle. Doing it using analytical techniques, we might divide the circle into segments and approximate the area of each segment with the area of a triangle. As the number of segments gets higher and higher, the sum of the areas of all triangles will approximate the area of the circle. The following figures demonstrate the idea of creating infinitely many vanishingly small triangles to get the (finite) total area of a circle.

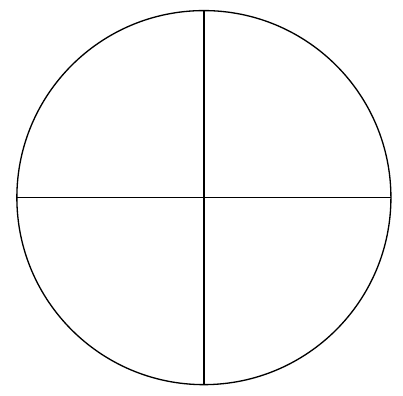
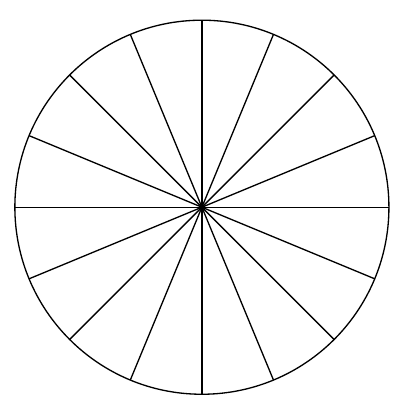
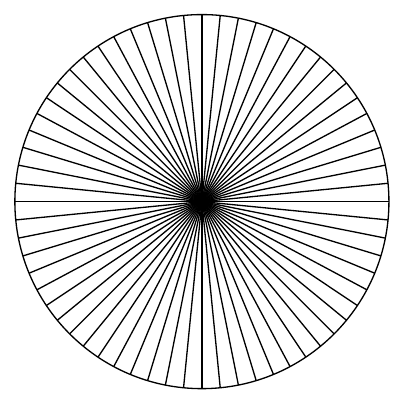
Theoretical minimum (in a nutshell)

You should be acquainted with set theory, especially the set operations and basics about functions.

Concepts you will learn in this part of BookofProofs

• real analysis of one variable, addressing basic analytical concepts for the calculus of one real variable.
• real analysis of multiple variables, addressing basic analytical concepts for the calculus of more than one real variable.
• complex analysis, dealing with complex numbers and also known as the _theory of functions
• differential equations, dealing with equations containing an unknown function as a derivative and providing a theory capable to describe many physical phenomena,
• linear integral equations, dealing with equations containing the unknown function under the integral
• functional analysis, discussing modern theories of differentiation and integration and the principal problems and methods of handling integral and linear functionals
• vector analysis, concerned with differentiation and integration of vector fields
• calculus of variations, which is concerned with the problem of "extremising" functionals.

Table of Contents

1. Part: Historical Development of Analysis
2. Part: Real Analysis of One Variable and Elements of Complex Analysis
3. Part: Real Analysis of Multiple Variables
4. Part: Complex Analysis
5. Part: Differential Equations
6. Part: Linear Integral Equations
7. Part: Functional Analysis
8. Part: Calculus of Variations
9. Part: Vector Analysis

Mentioned in:

Definitions: 1
Parts: 2 3 4 5

Thank you to the contributors under CC BY-SA 4.0!

Github:

References

Bibliography

1. Govers, Timothy: "The Princeton Companion to Mathematics", Princeton University Press, 2008,