Where a large number of workmen are employed on a building it is customary to provide every man with a little disc bearing his number. These are hung on a board by the men as they arrive, and serve as a check on punctuality. Now, I once noticed a foreman remove a number of these checks from his board and place them on a split-ring which he carried in his pocket. This at once gave me the idea for a good puzzle. In fact, I will confide to my readers that this is just how ideas for puzzles arise. You cannot really create an idea: it happens—and you have to be on the alert to seize it when it does so happen.
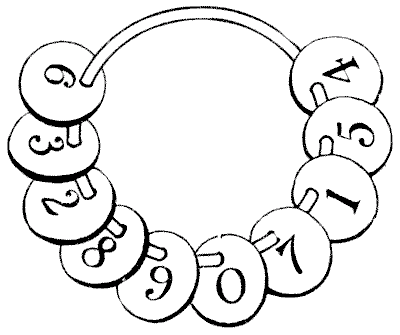
It will be seen from the illustration that there are ten of these checks on a ring, numbered $1$ to $9$ and $0.$ The puzzle is to divide them into three groups without taking any off the ring so that the first group multiplied by the second makes the third group. For example, we can divide them into the three groups, $2—897—15463,$ by bringing the $6$ and the $3$ round to the $4,$ but unfortunately, the first two when multiplied together do not make the third. Can you separate them correctly? Of course, you may have as many of the checks as you like in any group. The puzzle calls for some ingenuity unless you have the luck to hit on the answer by chance.
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.