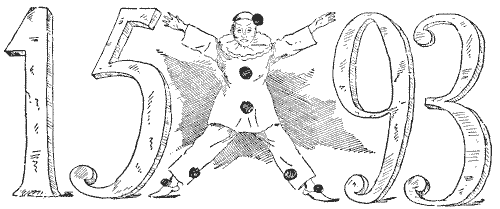
The Pierrot in the illustration is standing in a posture that represents the sign of multiplication. He is indicating the peculiar fact that $15$ multiplied by $93$ produces exactly the same figures ($1,395$), differently arranged. The puzzle is to take any four digits you like (all different) and similarly arrange them so that the number formed on one side of the Pierrot when multiplied by the number on the other side shall produce the same figures. There are very few ways of doing it, and I shall give all the cases possible. Can you find them all? You are allowed to put two figures on each side of the Pierrot as in the example shown or to place a single figure on one side and three figures on the other. If we only used three digits instead of four, the only possible ways are these: $3$ multiplied by $51$ equals $153,$ and $6$ multiplied by $21$ equals $126.$
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.