I will repeat that if a chessboard is cut into four equal parts, as indicated by the dark lines in the illustration, it is not possible to perform a knight's tour, either re-entrant or not, on one of the parts. The best re-entrant attempt is shown, in which each knight has to trespass twice on other parts.
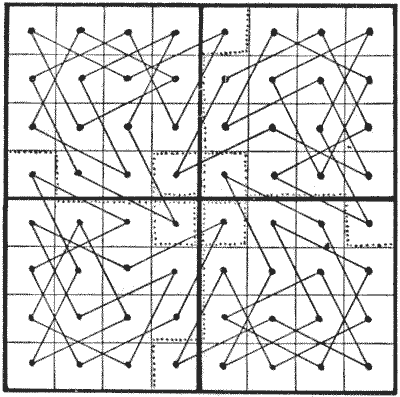
The puzzle is to cut the board differently into four parts, each of the same size and shape, so that a re-entrant knight's tour may be made on each part. Cuts along the dotted lines will not do, as the four central squares of the board would be either detached or hanging on by a mere thread.
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.