(related to Problem: The Lion And The Man)
First of all, the fewest possible straight lines in each case are twenty-two, and in order that no cell may be visited twice, it is absolutely necessary that each should pass into one cell and then immediately "visit" the one from which he started, afterwards proceeding by way of the second available cell. In the following diagram, the man's route is indicated by the unbroken lines, and the lion's by the dotted lines.
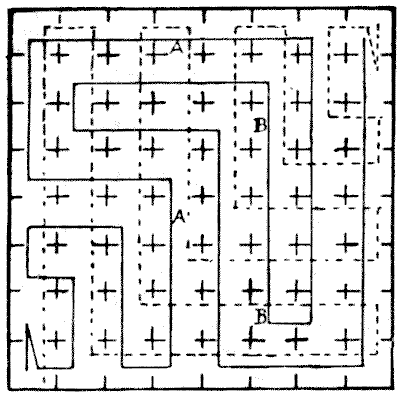
It will be found if the two routes are followed cell by cell with two pencil points, that the lion and the man never meet. But there was one little point that ought not to be overlooked—"they occasionally got glimpses of one another." Now, if we take one route for the man and merely reverse it for the lion, we invariably find that, going at the same speed, they never get a glimpse of one another. But in our diagram it will be found that the man and the lion are in the cells marked A at the same moment, and may see one another through the open doorways; while the same happens when they are in the two cells marked $B,$ the upper letters indicating the man and the lower the lion. In the first case the lion goes straight for the man, while the man appears to attempt to get in the rear of the lion; in the second case, it looks suspiciously like running away from one another!
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.