(related to Problem: Bachet's Square)
Let us use the letters $A, K, Q, J,$ to denote ace, king, queen, jack; and $D, S, H, C,$ to denote diamonds, spades, hearts, clubs. In Diagrams $1$ and $2$, we have the two available ways of arranging either group of letters so that no two similar letters shall be in line — although a quarter-turn of $1$ will give us the arrangement in $2.$
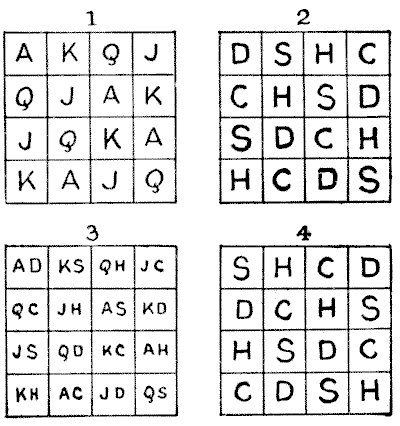
If we superimpose or combine these two squares, we get the arrangement of Diagram $3,$ which is one solution. But in each square, we may put the letters in the top line in twenty-four different ways without altering the scheme of arrangement.
Thus, in Diagram $4$ the $S$'s are similarly placed to the $D$'s in $2,$ the $H$'s to the $S$'s, the $C$'s to the $H$'s, and the $D$'s to the $C$'s. It clearly follows that there must be $24 \times 24 = 576$ ways of combining the two primitive arrangements. But the error that Labosne fell into was that of assuming that the $A, K, Q, J$ must be arranged in the form $1,$ and the $D, S, H, C$ in the form $2.$ He thus included reflections and half-turns, but not quarter-turns. They may obviously be interchanged. So that the correct answer is $2 \times 576 = 1,152,$ counting reflections and reversals as different. Put in another manner, the pairs in the top row may be written in $16 \times 9 \times 4 \times 1 = 576$ different ways, and the square then completed in $2$ ways, making $1,152$ ways in all.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.