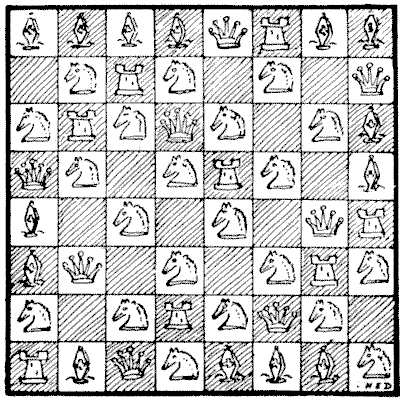
(related to Problem: The Crowded Chessboard)
Here is the solution. Only $8$ queens or $8$ rooks can be placed on the board without attack, while the greatest number of bishops is $14,$ and of knights $32.$ But as all these knights must be placed on squares of the same color, while the queens occupy four of each color and the bishops $7$ of each color, it follows that only $21$ knights can be placed on the same color in this puzzle. More than $21$ knights can be placed alone on the board if we use both colors, but I have not succeeded in placing more than $21$ on the "crowded chessboard." I believe the above solution contains the maximum number of pieces, but possibly some ingenious reader may succeed in getting in another knight.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.