(related to Problem: Boards With An Odd Number Of Squares)
There are fifteen different ways of cutting the $5\times 5$ board (with the central square removed) into two pieces of the same size and shape. Limitations of space will not allow me to give diagrams of all these, but I will enable the reader to draw them all out for himself without the slightest difficulty. At whatever point on the edge your cut enters, it must always end at a point on the edge, exactly opposite in a line through the center of the square. Thus, if you enter at the point $1$ (see Fig. $1$) at the top, you must leave at the point $1$ at the bottom. Now, $1$ and $2$ are the only two really different points of entry; if we use any others they will simply produce similar solutions. The directions of the cuts in the following fifteen
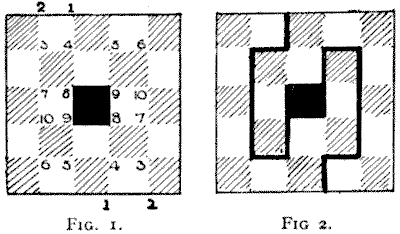
solutions are indicated by the numbers on the diagram. The duplication of the numbers can lead to no confusion since every successive number is contiguous to the previous one. But whichever direction you take from the top downwards you must repeat from the bottom upwards, one direction being an exact reflection of the other.
It will be seen that the fourth direction $(1, 4, 3, 7, 10, 6, 5, 9)$ produces the solution shown in Fig. $2.$ The thirteenth produces the solution given in propounding the puzzle, where the cut entered at the side instead of at the top. The pieces, however, will be of the same shape if turned over, which, as it was stated in the conditions, would not constitute a different solution.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.