(related to Problem: Chequered Board Divisions)
There are $255$ different ways of cutting the board into two pieces of exactly the same size and shape. Every way must involve one of the five cuts shown in Diagrams $A, B, C, D,$ and $E.$ To avoid repetitions by reversal and reflection, we need only consider cuts that enter at the points $a, b,$ and $c.$ But the exit must always be at a point in a straight line from the entry through the center. This is the most important condition to remember. In case $B$ you cannot enter at $a,$ or you will get the cut provided for in $E.$ Similarly, in $C$ or $D,$ you must not enter the key-line in the same direction as itself, or you will get $A$ or $B.$ If you are working on $A$ or $C$ and entering at $a,$ you must consider joins at one end only of the key-line, or you will get repetitions. In other cases, you must consider joins at both ends of the key; but after leaving $a$ in case $D,$ turn always either to right or left — use one direction only. Figs. $1$ and $2$ are examples under $A;$ $3$ and $4$ are examples under $B;$ $5$ and $6$ come under $C;$ and $7$ is a pretty example of $D.$ Of course, $E$ is a peculiar type, and obviously admits of only one way of cutting, for you clearly cannot enter at $b$ or $c.$
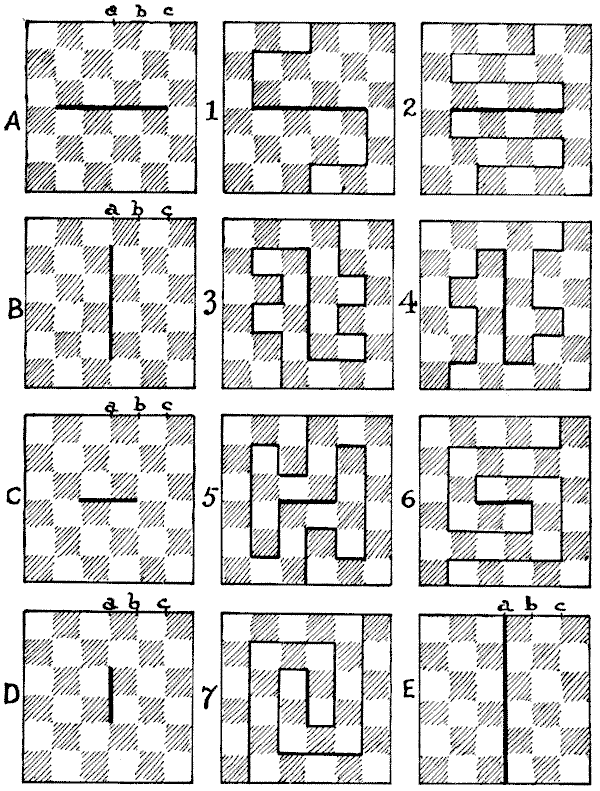
Here is a table of the results:— $$\begin{array}{ccrcrcrcr} &&a & &b& & c& &\text{Ways}\\ A& =& 8& +& 17& +& 21& =& 46\\ B &=& 0& +& 17& +& 21& =& 38\\ C &=& 15& +& 31& +& 39& =& 85\\ D& =& 17& +& 29& +& 39& =& 85\\ E &=& 1& +& 0& +& 0& = &1\\ \hline &&41&& 94&& 120&& 255 \end{array}$$
I have not attempted the task of enumerating the ways of dividing a board $8\times 8$ — that is, an ordinary chessboard. Whatever the method adopted, the solution would entail considerable labor.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.