Here is a little game of solitaire that is quite easy, but not so easy as to be uninteresting. You can either rule out the squares on a sheet of cardboard or paper, or you can use a portion of your chessboard. I have shown numbered counters in the illustration so as to make the solution easy and intelligible to all, but chess pawns or draughts will serve just as well in practice.
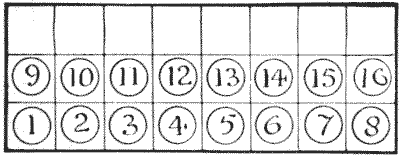
The puzzle is to remove all the counters except one, and this one that is left must be No. $1.$ You remove a counter by jumping over another counter to the next space beyond if that square is vacant, but you cannot make a leap in a diagonal direction. The following moves will make the play quite clear: $1—9,$ $2—10,$ $1—2,$ and so on. Here $1$ jumps over $9,$ and you remove $9$ from the board; then $2$ jumps over $10,$ and you remove $10;$ then $1$ jumps over $2,$ and you remove $2.$ Every move is thus a capture until the last capture of all is made by No. $1.$
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.