All that we need for this puzzle is nine counters, numbered $1, 2, 3, 4, 5, 6, 7, 8,$ and $9.$ It will be seen that in the illustration $A$ these are arranged so as to form a Greek cross, while in the case of $B$ they form a Latin cross. In both cases, the reader will find that the sum of the numbers in the upright of the cross is the same as the sum of the numbers in the horizontal arm.
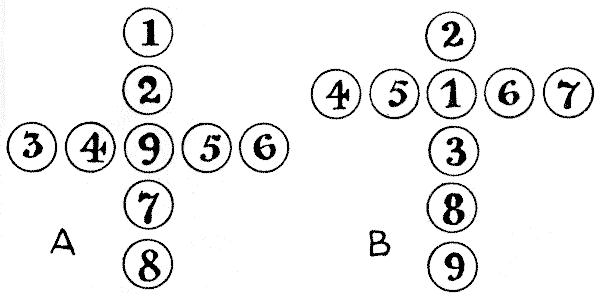
It is quite easy to hit on such an arrangement by trial, but the problem is to discover in exactly how many different ways it may be done in each case. Remember that reversals and reflections do not count as different. That is to say, if you turn this page round you get four arrangements of the Greek cross, and if you turn it around again in front of a mirror you will get four more. But these eight are all regarded as one and the same. Now, how many different ways are there in each case?
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.