(related to Problem: The Antiquary's Chain)
The number of ways in which nine things may be arranged in a row without any restrictions is $$1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8 \times 9 = 362,880.$$ But we are told that the two circular rings must never be together; therefore we must deduct the number of times that this would occur. The number is $$1 \times 2 \times 3 \times 4 \times 5 \times 6 \times 7 \times 8 = 40,320 \times 2 = 80,640,$$ because if we consider the two circular links to be inseparably joined together they become as one link, and eight links are capable of $40,320$ arrangements; but as these two links may always be put on in the orders $AB$ or $BA,$ we have to double this number, it being a question of arrangement and not of design. The deduction required reduces our total to $282,240.$ Then one of our links is of a peculiar form, like an $8.$ We have therefore the option of joining on either one end or the other on every occasion, so we must double the last result. This brings up our total to $564,480.$
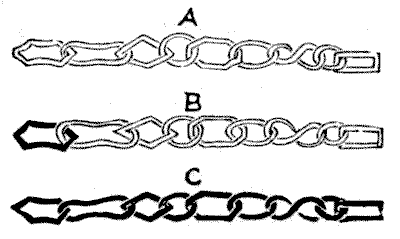
We now come to the point to which I directed the reader's attention — that every link may be put on in one of two ways. If we join the first finger and thumb of our left hand horizontally and then link the first finger and thumb of the right hand, we see that the right thumb may be either above or below. But in the case of our chain we must remember that although that 8-shaped link has two independent ends it is like every other link in having only two sides — that is, you cannot turn over one end without turning the other at the same time.
We will, for convenience, assume that each link has a black side and a side painted white. Now, if it was stipulated that (with the chain lying on the table, and every successive link falling over its predecessor in the same way, as in the diagram) only the white sides should be uppermost as in $A,$ then the answer would be $564,480,,$ as above — ignoring for the present all reversals of the completed chain. If, however, the first link were allowed to be placed either side up, then we could have either $A$ or $B,$ and the answer would be $2 \times 564,480 = 1,128,960;$ if two links might be placed either way up, the answer would be $4 \times 564,480;$ if three links, then $8 \times 564,480,$ and so on. Since, therefore, every link may be placed either side up, the number will be $564,480$ multiplied by $29,$ or by $512.$ This raises our total to $289,013,760.$
But there is still one more point to be considered. We have not yet allowed for the fact that with any given arrangement three of the other arrangements may be obtained by simply turning the chain over through its entire length and by reversing the ends. Thus $C$ is really the same as $A,$ and if we turn this page upside down, then $A$ and $C$ give two other arrangements that are still really identical. Thus to get the correct answer to the puzzle we must divide our last total by $4,$ when we find that there are just $72,253,440$ different ways in which the smith might have put those links together. In other words, if the nine links had originally formed a piece of chain, and it was known that the two circular links were separated, then it would be $72,253,439$ chances to $1$ that the smith would not have put the links together again precisely as they were arranged before!
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.