(related to Problem: The Fifteen Dominoes)
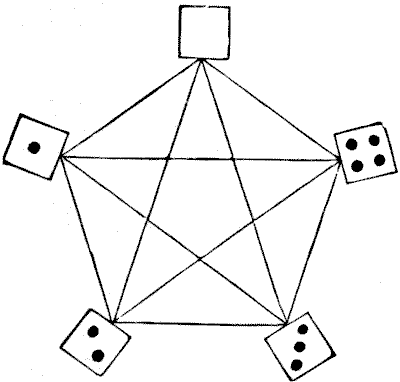
The reader may have noticed that at each end of the line I give is a four, so that, if we like, we can form a ring instead of a line. It can easily be proved that this must always be so. Every line arrangement will make a circular arrangement if we like to join the ends. Now, curious as it may at first appear, the following diagram exactly represents the conditions when we leave the doubles out of the question and devote our attention to forming circular arrangements. Each number, or half domino, is in line with every other number, so that if we start at any one of the five numbers and go over all the lines of the pentagon once and once only we shall come back to the starting place, and the order of our route will give us one of the circular arrangements for the ten dominoes. Take your pencil and follow out the following route, starting at the $4:$ $41304210234.$ You have been over all the lines once only, and by repeating all these figures in this way, $$41—13—30—04—42—21—10—02—23—34,$$ you get an arrangement of the dominoes (without the doubles) which will be perfectly clear. Take other routes and you will get other arrangements. If, therefore, we can ascertain just how many of these circular routes are obtainable from the pentagon, then the rest is very easy.
Well, the number of different circular routes over the pentagon is $264.$ How I arrive at these figures I will not at present explain, because it would take a lot of space. The dominoes may, therefore, be arranged in a circle in just $264$ different ways, leaving out the doubles. Now, in any one of these circles, the five doubles may be inserted in $25 = 32$ different ways. Therefore when we include the doubles there are $264 \times 32 = 8,448$ different circular arrangements. But each of those circles may be broken (so as to form our straight line) in any one of $15$ different places. Consequently, $8,448 \times 15$ gives $126,720$ different ways as the correct answer to the puzzle.
I purposely refrained from asking the reader to discover in just how many different ways the full set of twenty-eight dominoes may be arranged in a straight line in accordance with the ordinary rules of the game, left to right and right to left of any arrangement counting as different ways. It is an exceedingly difficult problem, but the correct answer is $7,959,229,931,520$ ways. The method of solving is very complex.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.