(related to Problem: The Cross and the Triangle)
The line $A B$ in the following diagram represents the side of a square having the same area as the cross. I have shown elsewhere, as stated, how to make a square and equilateral triangle of equal area. I need not go, therefore, into the preliminary question of finding the dimensions of the triangle that is to equal our cross. We will assume that we have already found this, and the question then becomes, How are we to cut up one of these into pieces that will form the other?
First, draw the line $A B$ where $A$ and $B$ are midway between the extremities of the two side arms. Next, make the lines $D C$ and $E F$ equal in length to half the side of the triangle. Now from $E$ and $F$ describe with the same radius the intersecting arcs at $G$ and draw $F G.$ Finally, make $I K$ equal to $H C$ and $L B$ equal to $A D.$ If we now draw $I L,$ it should be parallel to $F G,$ and all the six pieces are marked out. These fit together and form a perfect equilateral triangle, as shown in the second diagram. Or we might have first found the direction of the line M N in our triangle, then placed the point $O$ over the point $E$ in the cross and turned around the triangle over the cross until the line $M N$ was parallel to $A B.$ The piece $5$ can then be marked off and the other pieces in succession.
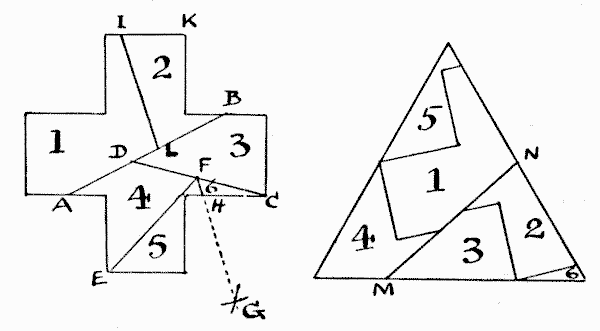
I have seen many attempts at a solution involving the assumption that the height of the triangle is exactly the same as the height of the cross. This is a fallacy: the cross will always be higher than the triangle of equal area.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.