(related to Problem: Linoleum Cutting)
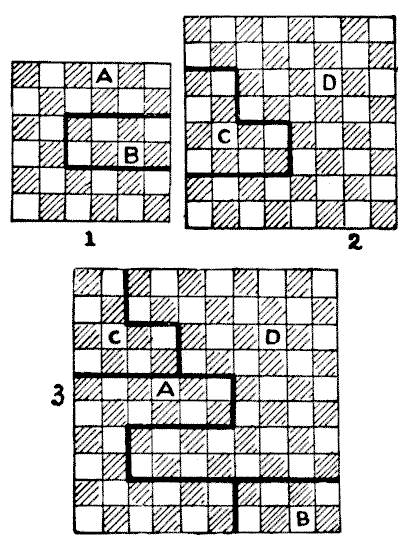
There is only one solution that will enable us to retain the larger of the two pieces with as little as possible cut from it. Fig. $1$ in the following diagram shows how the smaller piece is to be cut, and Fig. $2$ how we should dissect the larger piece, while in Fig. $3$ we have the new square $10 \times 10$ formed by the four pieces with all the chequers properly matched. It will be seen that the piece $D$ contains fifty-two chequers, and this is the largest piece that it is possible to preserve under the conditions.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.