(related to Problem: The Squares Of Brocade)
So far as I have been able to discover, there is only one possible solution to fulfill the conditions. The pieces fit together as in Diagram $1,$ Diagrams $2$ and $3$ showing how the two original squares are to be cut. It will be seen that the pieces $A$ and $C$ have twenty chequers each, and are therefore of equal area.

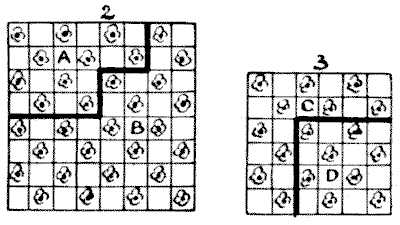
Diagram $4$ (built up with the dissected square No. $5$) solves the puzzle, except for the small condition contained in the words, "I cut the two squares in the manner desired." In this case, the smaller square is preserved intact. Still, I give it as an illustration of a feature of the puzzle.

It is impossible in a problem of this kind to give a quarter-turn to any of the pieces if the pattern is to properly match, but (as in the case of $F,$ in Diagram $5$) we may give a symmetrical piece a half-turn — that is, turn it upside down.

Whether or not a piece may be given a quarter-turn, a half-turn, or no turn at all in these chequered problems, depends on the character of the design, on the material employed, and also on the form of the piece itself.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.