(related to Problem: The Barrel Puzzle)
All that is necessary is to tilt the barrel as in Fig. $1,$ and if the edge of the surface of the water exactly touches the lip $a$ at the same time that it touches the edge of the bottom $b,$ it will be just half full. To be more exact, if the bottom is an inch or so from the ground, then we can allow for that, and the thickness of the bottom, at the top. If when the surface of the water reached the lip $a$, it had risen to the point $c$ in Fig. $2,$ then it would be more than half full. If, as in Fig. $3,$ some portion of the bottom were visible and the level of the water fell to the point $d,$ then it would be less than half full.
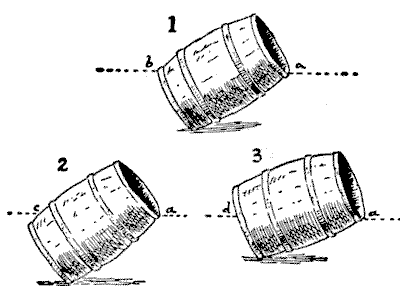
This method applies to all symmetrically constructed vessels.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.