(related to Problem: Cherries And Plums)
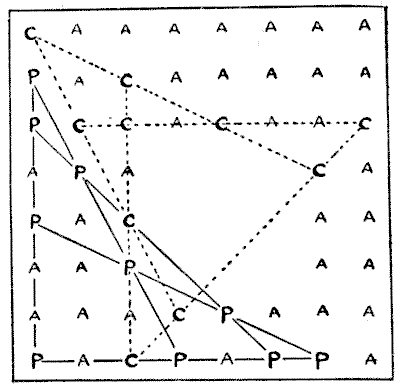
There are several ways in which this problem might be solved were it not for the condition that as few cherries and plums as possible shall be planted on the north and east sides of the orchard. The best possible arrangement is that shown in the diagram, where the cherries, plums, and apples are indicated respectively by the letters $C,$ $P,$ and $A.$ The dotted lines connect the cherries, and the other lines the plums. It will be seen that the ten cherry trees and the ten plum trees are so planted that each fruit forms five lines with four trees of its kind in line. This is the only arrangement that allows for so few as two cherries or plums being planted on the north and east outside rows.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.