(related to Problem: The Ten Coins)
The answer is that there are just $2,400$ different ways. Any three coins may be taken from one side to combine with one coin taken from the other side. I give four examples on this and the next page. We may thus select three from the top in ten ways and one from the bottom in five ways, making fifty. But we may also select three from the bottom and one from the top in fifty ways. We may thus select the four coins in one hundred ways, and the four removed may be arranged by permutation in twenty-four ways. Thus there are $24 \times 100 = 2,400$ different solutions.
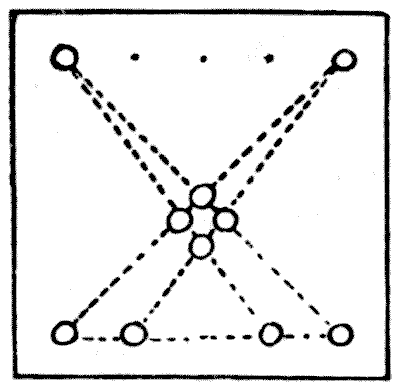
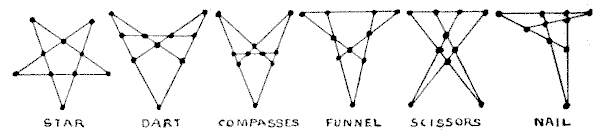
As all the points and lines puzzles that I have given so far, excepting the last, are variations of the case of ten points arranged to form five lines of four, it will be well to consider this particular case generally. There are six fundamental solutions, and no more, as shown in the six diagrams. These, for the sake of convenience, I named some years ago the Star, the Dart, the Compasses, the Funnel, the Scissors, and the Nail. Readers will understand that any one of these forms may be distorted in an infinite number of different ways without destroying its real character.
In "The King and the Castles" we have the Star, and its solution gives the Compasses. In the "Cherries and Plums" solution we find that the Cherries represent the Funnel and the Plums the Dart. The solution of the "Plantation Puzzle" is an example of the Dart distorted. Any solution to the "Ten Coins" will represent the Scissors. Thus examples of all have been given except the Nail.
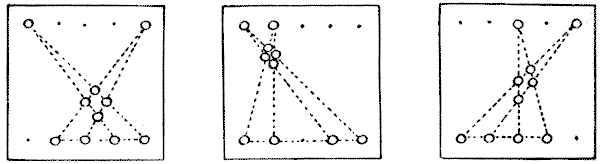
On a reduced chessboard, $7$ by $7,$ we may place the ten pawns in just three different ways, but they must all represent the Dart. The "Plantation" shows one way, the Plums show a second way, and the reader may like to find the third way for himself. On an ordinary chessboard, $8$ by $8,$ we can also get in a beautiful example of the Funnel — symmetrical in relation to the diagonal of the board. The smallest board that will take a Star is one $9$ by $7.$ The Nail requires a board $11$ by $7,$ the Scissors $11$ by $9,$ and the Compasses $17$ by $12.$ At least these are the best results recorded in my notebook. They may be beaten, but I do not think so. If you divide a chessboard into two parts by a diagonal zigzag line, so that the larger part contains $36$ squares and the smaller part $28$ squares, you can place three separate schemes on the larger part and one on the smaller part (all Darts) without their conflicting — that is, they occupy forty different squares. They can be placed in other ways without a division of the board. The smallest square board that will contain six different schemes (not fundamentally different), without any line of one scheme crossing the line of another, is $14$ by $14;$ and the smallest board that will contain one scheme entirely enclosed within the lines of a second scheme, without any of the lines of the one, when drawn from point to point, crossing a line of the other, is $14$ by $12.$
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.