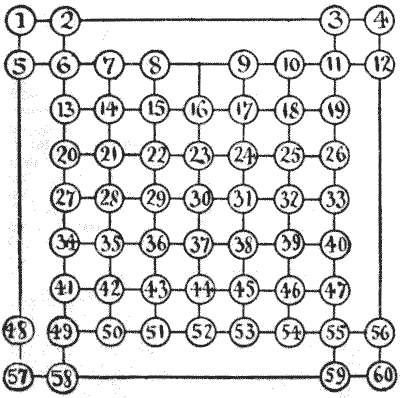
This variation of the last puzzle is also played by two persons. One puts a counter on No. $6,$ and the other puts one on No. $55,$ and they play alternately by removing the counter to any other number in a line. If your opponent moves at any time on to one of the lines you occupy or even crosses one of your lines, you immediately capture him and win. We will take an illustrative game. $A$ moves from $55$ to $52;$ $B$ moves from $6$ to $13;$ $A$ advances to $23;$ $B$ goes to $15;$ $A$ retreats to $26;$ $B$ retreats to $13;$ $A$ advances to $21;$ $B$ retreats to $2;$ $A$ advances to $7;$ $B$ goes to $3;$ $A$ moves to $6;$ $B$ must now go to $4;$ $A$ establishes himself at $11,$ and $B$ must be captured next move because he is compelled to cross a line on which $A$ stands. Play this over and you will understand the game directly. Now, the puzzle part of the game is this: Which player should win, and how many moves are necessary?
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.