(related to Problem: A Chessboard Fallacy)
The explanation of this little fallacy is as follows. The error lies in assuming that the little triangular piece, marked $C,$ is exactly the same height as one of the little squares of the board. As a matter of fact, its height (if we make the sixty-four squares each a square inch) will be $1\frac{1}{7}$ in. Consequently, the rectangle is really $9\frac{1}{7}$ in. by $7$ in., so that the area is sixty-four square inches in either case. Now, although the pieces do fit together exactly to form the perfect rectangle, yet the directions of the horizontal lines in the pieces will not coincide.
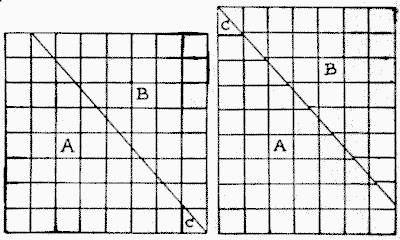
The new diagram above will make everything quite clear to the reader.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.