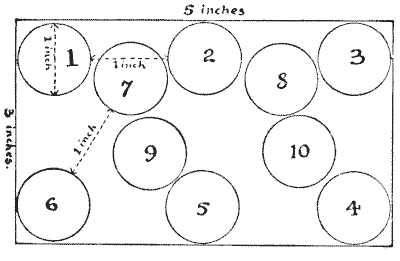
Here is an interesting little puzzle suggested to me by Mr. W. T. Whyte. Mark off on a sheet of paper a rectangular space $5$ inches by $3$ inches, and then find the greatest number of halfpennies that can be placed within the enclosure under the following conditions. A halfpenny is exactly an inch in diameter. Place your first halfpenny where you like, then place your second coin at exactly the distance of an inch from the first, the third an inch distance from the second, and so on. No halfpenny may touch another halfpenny or cross the boundary. Our illustration will make the matter perfectly clear. No. $2$ coin is an inch from No. $1;$ No. $3$ an inch from No. $2;$ No. $4$ an inch from No. $3;$ but after No. $10$ is placed we can go no further in this attempt. Yet several more halfpennies might have been got in. How many can the reader place?
Solutions: 1
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.