(related to Problem: The Monk And The Bridges)
The problem of the Bridges may be reduced to the simple diagram shown in the illustration. The point $M$ represents the Monk, the point $I$ the Island, and the point $Y$ the Monastery. Now, the only direct ways from $M$ to $I$ are by the bridges $a$ and $b;$ the only direct ways from $I$ to $Y$ are by the bridges $c$ and $d;$ and there is a direct way from $M$ to $Y$ by the bridge $e.$ Now, what we have to do is to count all the routes that will lead from $M$ to $Y,$ passing over all the bridges, $a, b, c, d,$ and $e$ once and once only. With the simple diagram under the eye it is quite easy, without any elaborate rule, to count these routes methodically.
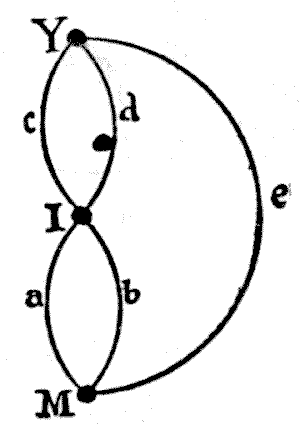
Thus, starting from $a, b,$ we find there are only two ways of completing the route; with $a, c,$ there are only two routes; with $a, d,$ only two routes; and so on. It will be found that there are sixteen such routes in all, as in the following list:— $$\begin{array}{c}a b e c d\\ a b e d c\\ a c d b e\\ a c e b d\\ a d e b c\\ a d c b e\\ b a e c d\\ b a e d c\\ b c d a e\\ b c e a d\\ b d c a e\\ b d e a c\\ e c a b d\\ e c b a d\\ e d a b c\\ e d b a c\\ \end{array}$$
If the reader will transfer the letters indicating the bridges from the diagram to the corresponding bridges in the original illustration, everything will be quite obvious.
This eBook is for the use of anyone anywhere in the United States and most other parts of the world at no cost and with almost no restrictions whatsoever. You may copy it, give it away or re-use it under the terms of the Project Gutenberg License included with this edition or online at http://www.gutenberg.org. If you are not located in the United States, you'll have to check the laws of the country where you are located before using this ebook.