◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--1-plane-geometry / Proposition: 1.25: Angles and Sides in a Triangle IV

Proposition: 1.25: Angles and Sides in a Triangle IV

(Proposition 25 from Book 1 of Euclid's “Elements”)

If two triangles have two sides equal to two sides, respectively, but (one) has a base greater than the base (of the other), then (the former triangle) will also have the angle encompassed by the equal straight lines greater than the (corresponding) angle (in the latter).

• Let $ABC$ and $DEF$ be two triangles having the two sides $AB$ and $AC$ equal to the two sides $DE$ and $DF$, respectively (That is), $AB$ (equal) to $DE$, and $AC$ to $DF$.
• And let the base $BC$ be greater than the base $EF$.
• I say that angle $BAC$ is also greater than $EDF$.

Modern Formulation

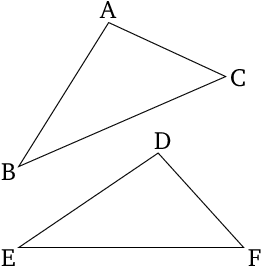
If two triangles (\(\triangle{ABC}\), \(\triangle{DEF}\)) have two sides of one triangle (\(\overline{AB}\), \(\overline{AC}\)) respectively equal to two sides of the other (\(\overline{DE}\), \(\overline{DF}\)), where the base of one \((\overline{BC})\) is greater than the base of the other \((\overline{EF})\), then the angle \((\angle{BAC})\) contained by the sides of the triangle with the longer base \((\triangle{ABC})\) is greater in measure than the angle \((\angle{EDF})\) contained by the sides of the other triangle \((\triangle{DEF})\).

In shorter words, if \(\overline{AB}=\overline{DE}\), \(\overline{AC}=\overline{DF}\), and \(\overline{BC} > \overline{EF}\), then \(\angle{BAC} > \angle{EDF}\).¹

Table of Contents

Proofs: 1 Corollaries: 1

Mentioned in:

Proofs: 1 2 3

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Calahan

@Casey

@Fitzpatrick

References

Adapted from CC BY-SA 3.0 Sources:

1. Callahan, Daniel: "Euclid’s 'Elements' Redux" 2014

Adapted from (Public Domain)

1. Casey, John: "The First Six Books of the Elements of Euclid"

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"

Footnotes