And that if a straight line falling across two (other) straight lines makes internal angles on the same side (of itself whose sum is) less than two right angles, then the two (other) straight lines, being produced to infinity, meet on that side (of the original straight line) that the (sum of the internal angles) is less than two right angles (and do not meet on the other side).1
if $\alpha+\beta < 180^\circ,$
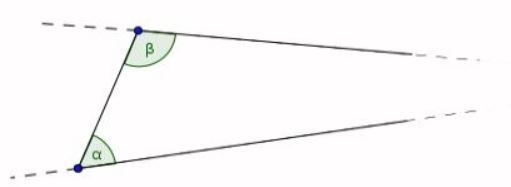
then

In a plane, through a given point \(A\) lying not on a given straight line \(g\), exactly one straight line \(h\) can be drawn, which is parallel to the given straight line.
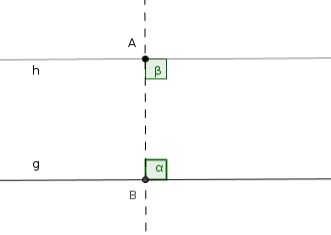
In my opinion, from the standpoint of a modern axiomatic method, the 5th postulate could be removed from the “Elements” without changing their validity! As far as I'm aware of, this observation is new and has never been dealt with in literature. I would appreciate receiving any comment, please contact me.
This is why:
This postulate effectively specifies that we are dealing with the geometry of flat, rather than curved, space. ↩
The formulations are equivalent, since only if the straight lines \(g\) and \(h\) are parallel, the segment \(AB\) is perpendicular to both straight lines (i.e. the angles \(\alpha,\beta\) are right angles). In other words, every other straight line drawn through the point \(A\) would cause the angle \(\beta\) to become either obtuse or acute. If it became acute, we would have the situation of the first formulation. If it became obtuse, the same formulation would apply for the supplemental angles of \(\alpha\) and \(\beta\). ↩