◀ ▲ ▶Branches / Geometry / Elements-euclid / Book--1-plane-geometry / Proposition: 1.33: Parallel Equal Segments Determine a Parallelogram

Proposition: 1.33: Parallel Equal Segments Determine a Parallelogram

(Proposition 33 from Book 1 of Euclid's “Elements”)

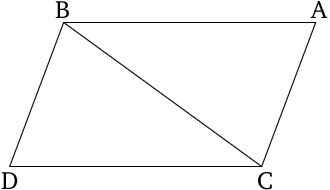
Straight-lines joining equal and parallel (straight lines) on the same sides are themselves also equal and parallel.

• Let $AB$ and $CD$ be equal and parallel (straight lines), and let the straight lines $AC$ and $BD$ join them on the same sides.
• I say that $AC$ and $BD$ are also equal and parallel.

Modern Formulation

Let \(\overline{AB}\), \(\overline{CD}\) be two equal parallel segments. Then the segments joining their adjacent endpoints, (\(\overline{AC}, \overline{BD}\)) are themselves parallel and equal in length: \(\overline{AC}=\overline{BD}\) and \(\overline{AC}\parallel\overline{BD}\). In other words, the quadrilateral \({ABCD}\) forms a parallelogram.

Table of Contents

Proofs: 1

Mentioned in:

Proofs: 1 2 3 4 5 6

Thank you to the contributors under CC BY-SA 4.0!

Github:

non-Github:

@Calahan

@Casey

@Fitzpatrick

References

Adapted from CC BY-SA 3.0 Sources:

1. Callahan, Daniel: "Euclid’s 'Elements' Redux" 2014

Adapted from (Public Domain)

1. Casey, John: "The First Six Books of the Elements of Euclid"

Adapted from (subject to copyright, with kind permission)

1. Fitzpatrick, Richard: Euclid's "Elements of Geometry"