Proof: By Euclid

For let the two straight lines joined to one another, $AB$ and $BC$, be (respectively) parallel to the two straight lines joined to one another, $DE$ and $EF$, (but) not in the same plane.
I say that angle $ABC$ is equal to (angle) $DEF$.

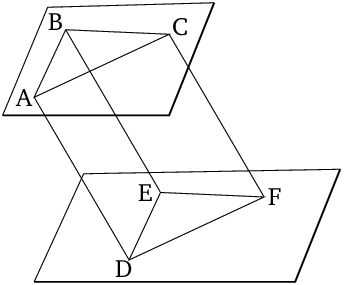
fig10e

For let $BA$, $BC$, $ED$, and $EF$ have been cut off (so as to be, respectively) equal to one another.
And let $AD$, $CF$, $BE$, $AC$, and $DF$ have been joined.
And since $BA$ is equal and parallel to $ED$, $AD$ is thus also equal and parallel to $BE$ [Prop. 1.33].
So, for the same reasons, $CF$ is also equal and parallel to $BE$.
Thus, $AD$ and $CF$ are each equal and parallel to $BE$.
And straight lines parallel to the same straight line, and which are not in the same plane as it, are also parallel to one another [Prop. 11.9].
Thus, $AD$ is parallel and equal to $CF$.
And $AC$ and $DF$ join them.
Thus, $AC$ is also equal and parallel to $DF$ [Prop. 1.33].
And since the two (straight lines) $AB$ and $BC$ are equal to the two (straight lines) $DE$ and $EF$ (respectvely), and the base $AC$ (is) equal to the base $DF$, the angle $ABC$ is thus equal to the (angle) $DEF$ [Prop. 1.8].
Thus, if two straight lines joined to one another are (respectively) parallel to two straight lines joined to one another, (but are) not in the same plane, then they will contain equal angles.
(Which is) the very thing it was required to show.
∎

Thank you to the contributors under CC BY-SA 4.0!